問題
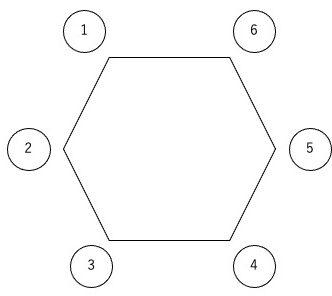
P、Q、R、Sの4人が、①〜⑥と書かれたスペースの上に立つ。
Pは4番か5番の上に立ったとすると、4人の場所の組み合わせは何通りか。
選択肢
- A. 24
- B. 72
- C. 120
- D. 240
- E. 720
編集者からワンポイントアドバイス
非言語の場合の数の問題は、情報を適切に把握する力が求められます。このような複数の条件が提示されている問題では、条件が厳しいものから考えていくことが重要です。
例えばこの問題では、P〜Sのうち、Pにだけ追加で条件が課されているため、Pから考えます。Pは④又は⑤の上に立つので、まず、④の上に立つ場合を考えてみましょう。そうすると、Q,R,Sの三人が①〜③及び⑤〜⑥の五つのスペースの上に立つ可能性を考えればいいとわかるため、\({}_5P_3\)で60通りとなります。Pが⑤の上に立つ場合も同様に考えて、やはり60通りとなります。従って、求める通りは60+60=120で、120通りとわかります。
このように条件の厳しさを考慮し、考える順番を意識して解いてみましょう。
例えばこの問題では、P〜Sのうち、Pにだけ追加で条件が課されているため、Pから考えます。Pは④又は⑤の上に立つので、まず、④の上に立つ場合を考えてみましょう。そうすると、Q,R,Sの三人が①〜③及び⑤〜⑥の五つのスペースの上に立つ可能性を考えればいいとわかるため、\({}_5P_3\)で60通りとなります。Pが⑤の上に立つ場合も同様に考えて、やはり60通りとなります。従って、求める通りは60+60=120で、120通りとわかります。
このように条件の厳しさを考慮し、考える順番を意識して解いてみましょう。