問題2-2（席・位置決め）

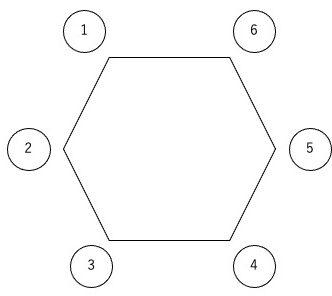
P、Q、R、S、Tの5人が、①〜⑥と書かれた座席に着く。

5人の座り方は何通りか。

 

区別された6つの席を5人が座るので、₆P₅ = 720通り。

非言語の場合の数の問題は、情報を適切に把握する力が求められます。このような情報を整理して理解する問題では、整理の仕方を工夫することが重要です。
例えばこの問題では、P〜Tの5人が①〜⑥の6席に着きますが、初めから誰がどこに座るかを決めていくと複雑になり混乱します。そのため、整理の仕方を工夫します。まず、座る席ではなく、座らない席を決めてみましょう。ここでは①の席には誰も座らないとします。そうすると、P〜Tが②〜⑥に座る仕方を求めればいいことになるため、\({}_5P_5＝120\)となり、①の席に座らない仕方は全部で120通りとわかります。②〜⑥も同様に考えると、求める場合の数は、\(120\times6＝720\)通りとなります。
このように整理の仕方を工夫することを意識して解いてみましょう。