問題2-3（席・位置決め）

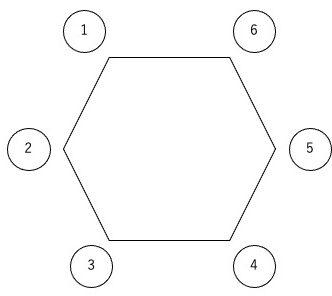
P、Q、R、Sの4人が、①〜⑥と書かれた丸椅子に座った。

4人の座り方は何通りか。

区別された6つの席を4人が座るので、₆P₄ = 360通り。

非言語の場合の数の問題は、情報を適切に把握する力が求められます。このような情報を整理して理解する問題では、問題の状況を具体的にイメージすることが重要です。
例えばこの問題では、①〜⑥の丸椅子にP〜Sが順番に座っていく行程をイメージしてみましょう。初めに、Pが座る場合を考えます。Pは①〜⑥の全ての丸椅子に座り得るので、可能性は6通りです。ここでは①に座ったとします。次に、Qが座る場合はどうでしょうか。既に①にはPが座っているため、選べる丸椅子は②〜⑥となり、可能性は5通りです。以下、Rは4通り、Sは3通りの座り方があるため、4人の座り方は、\(6\times5\times4\times3＝360\)で、360通りであるとわかります。
このように連続性を適切にイメージすることを意識して解いてみましょう。