問題2-5（席・位置決め）

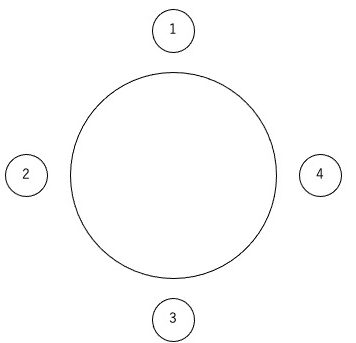
P、 Q、R、Sの4人が、①〜④と番号が振られた穴の中に入った。

PとQは向かい合った穴に入ったとすると、4人の入り方は何通りか。

 

PとQの組み合わせは順に、1と3、2と4、3と1、4と2の４通り。

PとQが1と3に入る場合：2番に入るのはRかSなので２通り。

PとQが2と4に入る場合：1番に入るのはRかSなので２通り。

というようにP、Qの入る場所が3と1、4と2の時も同様に計算できる。したがって、4人の入り方は4×2＝8通り。

非言語の場合の数の問題は、情報を適切に把握する力が求められます。このような複雑な条件が課されている問題では、抽象的に考えるのではなく、具体的なレベルに落とし込んで考えることが重要です。
例えば、この問題ではPとQは向かい合う、すなわち、Pの場所が決まると自動的にQの場所も確定するため、Pの入り得る穴を具体的に数え上げてみましょう。Pが①に入った場合、Qは③となり、残る②と④にRとSが入るため可能性は2通りとなります。Pが②に入った場合、Qは④となり、残る①と③にRとSが入るため可能性は2通りとなります。Pが③、④の場合も同様に考えて、それぞれ2通りとなるので、求める場合の数は\(2\times4＝8\)で、8通りとわかります。
このように時には具体的に数え上げることも有効な手段のひとつです。