問題3-6（集合）

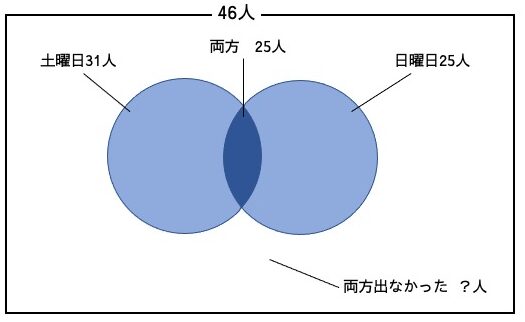
部活のメンバー46人のうち、土曜日に試合に出た人は31人、出なかった人は15人だった。また、日曜日の試合に出た人は25人、出なかった人は21人だった。

土曜日も日曜日も試合に出なかった人は最大で何人か。

正解：

C. 15

あなたの回答:

両方の試合に出た人は図の濃い青い部分であり、土曜日の参加者が31人、日曜日の参加者が25人であることから最大で25人である。

このとき、両方の試合に出なかった人の人数も最大になるので、求めるべき人数は、

46 – (31 + 25 – 25 ) = 15 人

 

 

 

非言語の集合の問題は、多層的な情報を処理する能力が求められます。このような重なり合った複数の情報を分析する問題では、ベン図を描くことが重要です。
例えばこの問題では、土曜日に試合に出た人の集合をX、日曜日のそれをYとして考えてみましょう。まず、部員数が46人であることから、XとYの共通部分には最小で10人、最大で25人が属すことがわかり、この中から、両日試合に出ない人の数が最も大きくなる場合を探します。例えば、共通部分が10人だった場合、XとYの集合に46人全員が属すことになり、両日試合に出なかった人は0人となります。逆に、共通部分が25人だった場合、XとYに属す人の合計は31人となり、両日試合に出なかった人は15人となります。従って、答えは15人とわかります。
尚、共通部分が25人ということはXがYを完全に包含しているので、Xに属さないならYに属さないといえます。そのため、どちらにも属さない人の数が最も大きくなります。