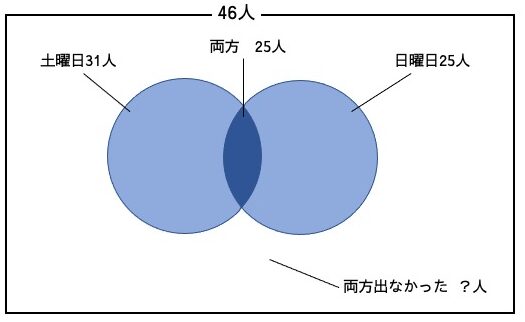
部活のメンバー46人のうち、土曜日に試合に出た人は31人、出なかった人は15人だった。また、日曜日の試合に出た人は25人、出なかった人は21人だった。

土曜日、日曜日の両方の試合に出た人は最も多くて何人か。

 

正解：

D. 25

あなたの回答:

土曜日に試合に出た人が31人、日曜日に試合に出た人が25人なので最大で25人。

非言語の集合の問題は、多層的な情報を処理する能力が求められます。このような重なり合った複数の情報を分析する問題では、ベン図を描くことが重要です。
例えばこの問題では、土曜日に試合に出た人の集合をX、日曜日に試合に出た人の集合をYとして考えてみましょう。この問題で問われているのは、土日の両方で試合に出得る人の最大値です。これは乃ち、XとYの共通部分が最も大きくなる場合を求めるということです。そこでふたつの集合の共通部分について考えてみると、それが最も大きくなるのは、一方の集合が他方の集合を完全に包含している時だとわかります。従って、この問題では、より大きな集合Xがより小さな集合Yを完全に包含している時が答えだとわかるので、答えは25人だとわかります。
この様に、集合同士の関係を比較検討しながら解いてみましょう。

部活のメンバー46人のうち、土曜日に試合に出た人は31人、出なかった人は15人だった。また、日曜日の試合に出た人は25人、出なかった人は21人だった。

土曜日も日曜日も試合に出なかった人は最大で何人か。

正解：

C. 15

あなたの回答:

両方の試合に出た人は図の濃い青い部分であり、土曜日の参加者が31人、日曜日の参加者が25人であることから最大で25人である。

このとき、両方の試合に出なかった人の人数も最大になるので、求めるべき人数は、

46 – (31 + 25 – 25 ) = 15 人

 

 

 

非言語の集合の問題は、多層的な情報を処理する能力が求められます。このような重なり合った複数の情報を分析する問題では、ベン図を描くことが重要です。
例えばこの問題では、土曜日に試合に出た人の集合をX、日曜日のそれをYとして考えてみましょう。まず、部員数が46人であることから、XとYの共通部分には最小で10人、最大で25人が属すことがわかり、この中から、両日試合に出ない人の数が最も大きくなる場合を探します。例えば、共通部分が10人だった場合、XとYの集合に46人全員が属すことになり、両日試合に出なかった人は0人となります。逆に、共通部分が25人だった場合、XとYに属す人の合計は31人となり、両日試合に出なかった人は15人となります。従って、答えは15人とわかります。
尚、共通部分が25人ということはXがYを完全に包含しているので、Xに属さないならYに属さないといえます。そのため、どちらにも属さない人の数が最も大きくなります。

中学生120人に野球、サッカー、テニスをやっているかどうかに関する調査を行った。野球、サッカー、テニスのどれもやっていない人が20人いた。また、野球もしくはサッカーをやっている人はテニスだけをやっている人の３倍いるとする。野球もしくはサッカーをやっている人の人数は何人か。

正解：

D. 75

あなたの回答:

求めるべき人数は上図の濃い青い部分。

野球もしくはサッカーをやっている人はテニスだけをやっている人の３倍であるから、それぞれ3x、xとおける。

これより、120 – 20 = 3x + x が成り立つから、これを解くとx= 25

よって求めるべき人数は3x = 75 人

 

 

非言語の集合の問題は、多層的な情報を処理する能力が求められます。このような重なり合った複数の情報を分析する問題では、ベン図を描くことが重要です。
例えばこの問題では、それぞれのスポーツをやっている人の集合を3つ描いて考えてみましょう。まず、何のスポーツもやっていない人が20人いるため、3つの集合のいずれかに属している人は100人だとわかります。ここで、テニスだけをやっている人の数をx、野球またはサッカーをやっている人の集合をyとします。すると、x＋y＝100と立式できます。また、問題文より3x＝yなので、これらよりy＝75となり、答えは75人とわかります。
この様に、ベン図を手がかりに情報を整理して、式を立てるなど工夫しながら解いてみましょう。