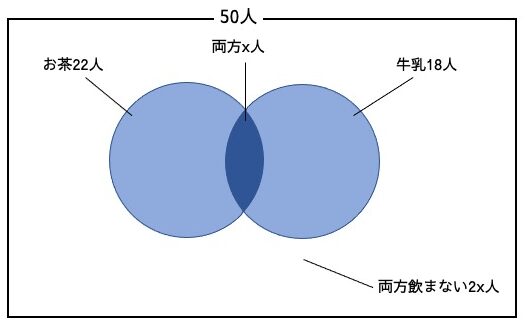
問題
都道府県X、Y、Zの1年間の交通事故にあった人を数えた。
表1は年齢別に人数を集計したもの、表2は都道府県X、Y、Zにおけるそれぞれの事故にあった人の割合を示したものである。
13歳から18歳の割合が最も高い都道府県はどれか。
表1

表2

選択肢
A. X
B. Y
C. Z
D. 表からは分からない
編集者からワンポイントアドバイス
例えばこの問題では、初めに?に入る数字を確定させます。Xの事故者の割合が44%に対して事故者数は1100人であることと、Yの事故者割合が30%であることから、Yの事故者数は750人となり、?に入るのは147とわかります。次に、Xの事故者は全体で1100人でそのうち300人が13-18歳なので割合は約27%となります。同様にYとZも対象の事故者数を全体の事故者数で割って、それぞれ約34%と約30%と分かるので、答えはYとなります。
この様に、全ての数字を先に確定させてから解くこともできます。