問題
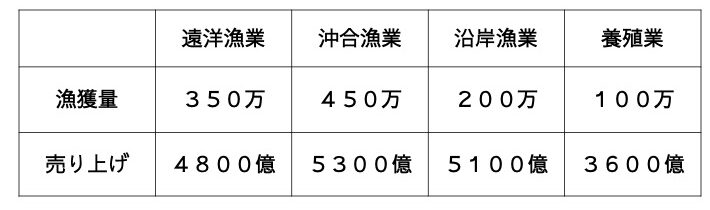
日本の漁獲量について、遠洋漁業、沖合漁業、沿岸漁業、養殖業に分けて集計した。以下の表は1975年と2015年にそれぞれについて調べたものであり、単位は全て(トン)である。
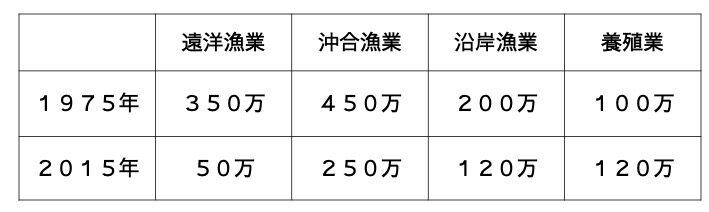
遠洋漁業、沖合漁業、沿岸漁業、養殖業の合計漁獲量に関して、2015年は1975年の何倍になっているか。必要であれば小数点第3位以下を四捨五入して答えよ。
選択肢
A. 0.25
B. 0.49
C. 1.43
D. 2.04
E. 3.55
編集者からワンポイントアドバイス
例えばこの問題では、両年の漁獲量の違いから答えの範囲をある程度予測することができます。1975年の合計漁獲量は1100万トンなのに対して、2015年のそれは540万トンです。ここで、2015年の漁獲量は1975年に比べて減っているので、倍率は1未満になるはずだということが予測できます。実際に計算してみると、\(540\div1100=0.4909…\)で、四捨五入して0.49倍となり、1倍より小さくなったのでこれが答えだとわかります。
この様に、与えられた情報から答えのヒントになるものを探しながら解いてみましょう。