問題7-1（表の読み取り）

問題

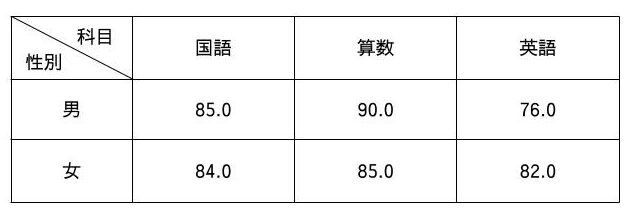
ある小学校の２年生が国語、算数、英語の３教科の試験を受けた。

男子学生の３教科の平均点はいくつか。（必要な時は、最後に小数点以下第２位を四捨五入すること）。

選択肢


  • A. 80.5

  • B. 83.3

  • C. 83.7

  • D. 86.6

  • E. 90.0

編集者からワンポイントアドバイス

非言語の表の読み取りの問題は、情報を適切に把握する力が求められます。このような情報を整理して理解する問題では、必要な情報を選択する力が重要です。
例えばこの問題では、男子学生の平均を求めたいので女子学生の記録は無視して解き進めることができます。平均を出したければ、各データの和をデータ数で割れば良いので85.0+90.0+76.0を3で割って83.66と6が無限に続くため、四捨五入して答えは83.7となります。

問題2-1（確率）

問題

 XとYの2人がくじをひく。そのくじは3等賞が当たる確率が\(\frac{1}{8}\)、4等賞の当たる確率が\(\frac{1}{4}\)である。XとYのうち片方が3等賞、もう片方が4等賞を当てる，という事象が起きる確率を求めよ。

 

選択肢


  • A. \(\frac{1}{32}\)

  • B. \(\frac{1}{16}\)

  • C. \(\frac{1}{8}\)

  • D. \(\frac{3}{8}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
この問題では、「XとYのうち片方が3等賞、もう片方が4等賞を当てる」という事象は、「Xが3等賞を当てYが4等賞を当てる」という事象と、「Yが3等賞を当てXが4等賞を当てる」という２つの事象に分けることができます。
このように求めたい事象を複数の事象に分けることを意識して問題を解いてみましょう。

問題2-2（確率）

問題

XとYがゲームをする。そのルールは，ルーレットを回し、出た数の大きい方が勝つというものである。このルーレットは1から8までの8つの整数が出て、それぞれの数字が出る確率は全て等しいとする。また、同じ数が出た場合は引き分けということにする。XがYに勝つ確率を求めよ。

 

選択肢


  • A. \(\frac{7}{16}\)

  • B. \(\frac{7}{8}\)

  • C. \(\frac{3}{8}\)

  • D. \(\frac{4}{5}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
確率の基本的な考え方とは求めたい特定の事象の場合の数を、全体の事象の場合の数で割ることです。この問題では、目の出方が8通りのルーレットをXとYがそれぞれ回すことが全体の事象であり、X＞Yが成り立つような違う数の2つの組み合わせが求めたい特定の事象にあたります。
分子にくる求めたい事象と分母の全体の事象が何であるのかを意識して問題を解いてみましょう。

問題2-3（確率）

問題

XとYが勝敗をかけてゲームをする。ルールは，ルーレットを回し、出た数の小さい方が負けというものである。このルーレットは1から8までの8つの整数が出て、それぞれの数字が出る確率は全て等しいとする。また、同じ数が出た場合は引き分けということにする。

Xが4以下を出してYに勝つ確率を求めよ。

選択肢


  • A. \(\frac{5}{32}\)

  • B. \(\frac{3}{32}\)

  • C. \(\frac{3}{16}\)

  • D. \(\frac{5}{16}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
確率の基本的な考え方とは求めたい特定の事象の場合の数を、全体の事象の場合の数で割ることです。この問題では、目の出方が8通りのルーレットをXとYがそれぞれ回すことが全体の事象であり、XもYも1から４の数から選ぶとしてX＞Yが成り立つような違う数の2つの組み合わせが求めたい特定の事象にあたります。
分子にくる求めたい事象と分母の全体の事象が何であるのかを意識して問題を解いてみましょう。

問題2-4（確率）

問題

XとYがダーツをする。そのルールは、刺さった場所に書いてある数の大きい方が勝つというものである。このダーツの的は1から8までが書かれている8つの場所があり、それぞれの数字の場所に当たる確率は全て等しいとする。また、同じ数の場所に刺した場合は引き分けということにする。

Xが5以上の差をつけてYに勝つ確率を求めよ。

 

選択肢


  • A. \(\frac{3}{64}\)

  • B. \(\frac{3}{16}\)

  • C. \(\frac{3}{32}\)

  • D. \(\frac{5}{32}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
確率の基本的な考え方とは求めたい特定の事象の場合の数を、全体の事象の場合の数で割ることです。この問題では、1から8までの8通りの出方があるダーツをXとYが行うことが全体の事象であり、Xが5以上の差をつけてYに勝つのが求めたい特定の事象にあたります。求めたい特定の事象に関しては、条件に該当する事象を全て書き出してみると良いでしょう。
分子にくる求めたい事象と分母の全体の事象が何であるのかを意識して問題を解いてみましょう。

問題2-6（確率）

問題

XとYがサッカーの試合を3回する。Xが勝つ確率、Yが勝つ確率、引き分けとなる確率は全て等しく\(\frac{1}{3} \)である。引き分けも試合数に数えるとする。Xが少なくとも1回勝つ確率を求めよ。

 

選択肢


  • A. \(\frac{8}{9}\)

  • B. \(\frac{26}{27}\)

  • C. \(\frac{5}{9}\)

  • D. \(\frac{19}{27}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
この問題では、「Xが少なくとも1回勝つ」という事象は、直接求めることが難しいため、余事象である「Xが3試合とも勝たない（Xの負けか引き分け）」を全体から引くと良いでしょう。
このように求めたい事象を直接求めることが難しい場合は余事象を活用することを意識して問題を解いてみましょう。

問題2-5（確率）

問題

XとYが野球の試合を3回する。Xが勝つ確率、Yが勝つ確率、引き分けとなる確率は全て等しく\(\frac{1}{3} \)である。引き分けも試合数に数えるとする。Xが2回勝ち、1回負ける確率を求めよ。

 

選択肢


  • A. \(\frac{1}{9}\)

  • B. \(\frac{1}{3}\)

  • C. \(\frac{2}{9}\)

  • D. \(\frac{1}{27}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
この問題では、「Xが2回勝ち、1回負ける」という事象を考える上で、まず「Xが1回目の試合で負けて残りは勝つ」という事象を考え、それと同様にXが負ける試合が2試合目、3試合目の場合をそれぞれ考えると良いでしょう。
このように求めたい事象を複数の事象に分けることを意識して問題を解いてみましょう。

問題2-7（確率）

問題

景品がもらえるくじをやる。当たりくじが2本、ハズレくじが6本入ったくじを8回ひく。ただし、一度引いたくじは元に戻さないものとする。

1回目と2回目のどちらも当たりをひく確率を求めよ。

 

選択肢


  • A. \(\frac{1}{28}\)

  • B. \(\frac{1}{56}\)

  • C. \(\frac{3}{28}\)

  • D. \(\frac{1}{7}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
この問題では、「1回目に当たりを引いてかつ2回目でも当たりを引く確率」として考えると良いでしょう。
このように求めたい事象をより求めやすい事象に置き換えることを意識して問題を解いてみましょう。

問題2-8（確率）

問題

当たりくじが2本、ハズレくじが6本入ったくじを8回ひく。ただし、一度引いたくじは元に戻さないものとする。

当たりを引くのが1回目または4回目である確率を求めよ。

 

選択肢


  • A. \(\frac{9}{28}\)

  • B. \(\frac{3}{14}\)

  • C. \(\frac{3}{28}\)

  • D. \(\frac{13}{28}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
確率の基本的な考え方とは求めたい特定の事象の場合の数を、全体の事象の場合の数で割ることです。この問題では、「8回のうち2回当たりを引き、残りの6回がハズレを引く」ということが全体の事象であり、「1回目と4回目のどちらか一方でのみ当たりをひくこと」が求めたい特定の事象にあたります。求めたい特定の事象に関しては、まず1回目に当たりを引き4回目にハズレを引くという事象を考えた上で、同様に1回目にハズレを引き4回目に当たりを引く事象を考えると良いでしょう。
分子にくる求めたい事象と分母の全体の事象が何であるのかを意識して問題を解いてみましょう。

問題2-9（確率）

問題

球が12個ある。赤色、青色、黄色、緑色の球が3つずつである。この袋の中から、同時にPとQが球を取り出す。1個ずつ取り出すものとする。2人とも赤色の球を取り出す確率を求めよ。

 

選択肢


  • A. \(\frac{3}{44}\)

  • B. \(\frac{1}{22}\)

  • C. \(\frac{1}{16}\)

  • D. \(\frac{1}{11}\)

編集者からワンポイントアドバイス

非言語の確率の問題ではその名の通り確率を求める問題が出題されます。確率は苦手意識を持つ人が多くいる単元ですが、基本的な考え方と想像力を持って考えることが問題を解くコツになります。
この問題では、PとQは球を同時に引くためPとQが同じ球を引くことはないといえます。よって「2人とも赤色の球を取り出す確率」は、「まずPが引いて残った球の中からQが引くとして、両者とも赤色の球を取り出す確率」として考えると良いでしょう。
このように求めたい事象をより求めやすい事象に置き換えることを意識して問題を解いてみましょう。